【Codewars每日一题】- Rectangle into Squares

题目

The drawing below gives an idea of how to cut a given “true” rectangle into squares (“true” rectangle meaning that the two dimensions are different).

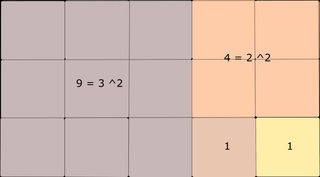
Rectangle into Squares

Can you translate this drawing into an algorithm?

You will be given two dimensions

a positive integer length (parameter named lng)
a positive integer width (parameter named wdth)

You will return an array with the size of each of the squares.

Shell bash returns a string.

Examples

sqInRect(5, 3) should return [3, 2, 1, 1]
sqInRect(3, 5) should return [3, 2, 1, 1]
sqInRect(20, 14) should return [14, 6, 6, 2, 2, 2]
sqInRect(5, 5) should return None

#Note: lng == wdth as a starting case would be an entirely different problem and the drawing is planned to be interpreted with lng != wdth.

思路

题目的含义是将一个长方形切割成正方形，且正方形尽可能的大。看返回值的规律应该是，将两个数值相减，直至两个数值相等。需要使用递归。

但是初步写完测试后，返现不是这个规律。sqInRect(20, 14) should return [14, 6, 6, 2, 2, 2]这个就不适用。

答案

我的答案

def sqInRect(lng, wdth):
    if lng == wdth:
        return None
    list = []
    
    list.append(min(lng, wdth))
    while lng != wdth:
        minNum = min(lng, wdth)
        maxNum = max(lng, wdth)
        lng = minNum
        wdth = maxNum - minNum
        list.append(min(lng, wdth))  
    return list

最佳答案

最佳实践解法

def sqInRect(lng, wdth):
    if lng == wdth:
        return None
    if lng < wdth:
        wdth, lng = lng, wdth
    res = []
    while lng != wdth:
        res.append(wdth)
        lng = lng - wdth
        if lng < wdth:
            wdth, lng = lng, wdth
    res.append(wdth)
    return res

递归的解法

# Recursive solution
def sqInRect(lng, wdth, recur = 0):
    if lng == wdth:
        return (None, [lng])[recur]            # If this is original function call, return None for equal sides (per kata requirement);
                                               # if this is recursion call, we reached the smallest square, so get out of recursion.
    lesser = min(lng, wdth)
    return [lesser] + sqInRect(lesser, abs(lng - wdth), recur = 1)